Method of Fractal Description (MFD)
In the case of complex...
...interconnected systems, as they usually are in the field of political institutions, processes and networks, we basically assume that a given question should be analysed using methods of holistic thinking. This procedure should then also have as high a hit rate as possible in order to grasp overall connections and to be able to derive conclusions from them with regard to the question.
Practice shows,
however, that the trained thinking structures lead to simplifying complex
processes and procedures as much as possible or breaking them down into partial
questions until an understanding of the facts associated with the question can
be derived from them. However, this approach usually involves a reduction of
the question or the issue that determines it to a linear (one-dimensional)
view, which usually leads to an incomplete, sometimes even wrong description.
The method of fractal analysis
The method of fractal analysis (MEFRA) is a very complex method that has been developed over many years by Emer. Prof. DDr. Helmut Detter over many years. His method of analysis, developed in theory and practice, allows a multidimensional description of complex and interconnected issues, which is helpful in political processes insofar as a growing number of influencing parameters have to be recorded, which have an effect on certain circumstances or have caused them.
In a political analysis, the use of MFD is
based on three steps - desk research, expert consultations, description of the
issue in fractal decomposition - as a basis for a qualified discussion and
further political analysis. In the practice of using MFD so far, the method of
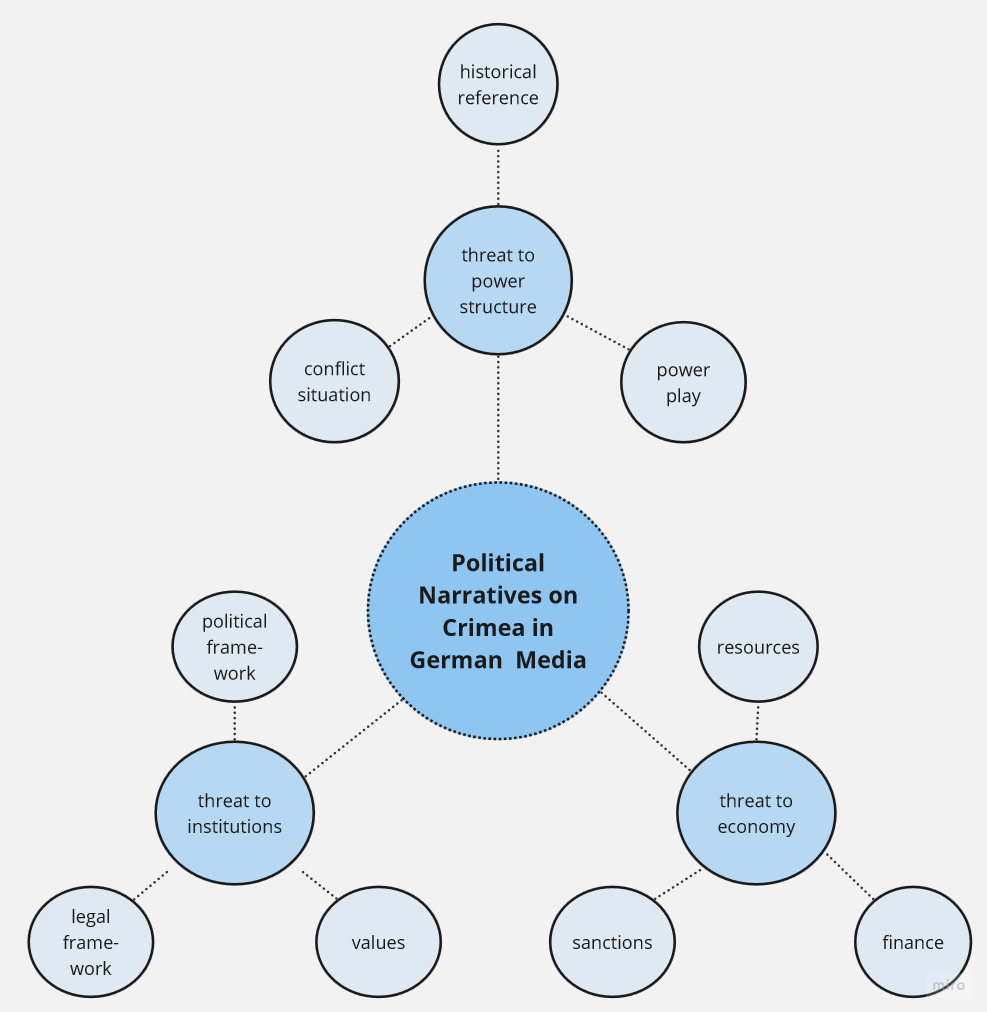
brainstorming has proven itself as an instrument in step 3. The aim of this
brainstorming process is to collect a set of influencing parameters that
describe the basic assumption.
These influencing parameters
The influence parameters must be identified with a high degree of accuracy. The reduction of the number to three results from the fact that the tripod represents a stable system in natural science. The self-similarity of the fractal allows the influence parameters to be described in ever greater detail. more detail.